Aplicaciones sencillas de wavelets

Éste pretende ser un comentario paralelo y dependiente de la introducción a las onditas en el excelente blog “El Mar dentro de un Caracol”. En él, quiero mostrar cómo las ideas presentadas por Gerard pueden usarse para encontrar aplicaciones a todo tipo de problemas tanto teóricos de la matemática más pura, como prácticos, propios de una ingeniería. Hoy voy a empezar por algo sencillo, sacado del campo de tratamiento de imágenes: Wavelets y Compresión.

Consideramos una imagen como una función simple del cuadrado unidad en los reales positivos, que de hecho tan sólo toma un número finito de valores; esta representación viene a corresponderse con la estructura matricial en pixels a la que tan acostumbrados estamos. Por ejemplo, la imagen que acompaña estas líneas viene a ser representada con una función simple tomando 1024×1024 = 1048576 valores, que van desde el cero (negro) hasta el 255 (blanco)—cualquier valor intermedio se corresponde con un diferente tono de gris. ¿Cómo usar la construcción que indicaba Gerard a base de “piezas de Lego” para comprimir dicha imagen?
Empezamos por una pieza que ocupe el cuadrado entero. Lo difícil aquí es calcular el valor numérico correspondiente al tono de gris que va a ocupar dicho lugar. Ahí es donde uno emplea la definición formal de ondita.

En el segundo paso, dividimos el anterior cuadrado en cuatro, cortando por los puntos medios de los lados, y colocamos una pieza del tamaño correspondiente en cada posición (es decir, añadimos en cada cuadrado recién creado un nuevo valor al anterior, así modificando el tono de gris que había previamente en cada región). Cada cuadrado es nuevamente dividido en cuatro usando el mismo procedimiento, y en cada nueva posición volvemos a colocar una nueva pieza. Al cabo de estos tres pasos iniciales, hemos colocado 1 + 4 + 16 = 21 piezas, y tenemos la sucesión de imágenes siguiente: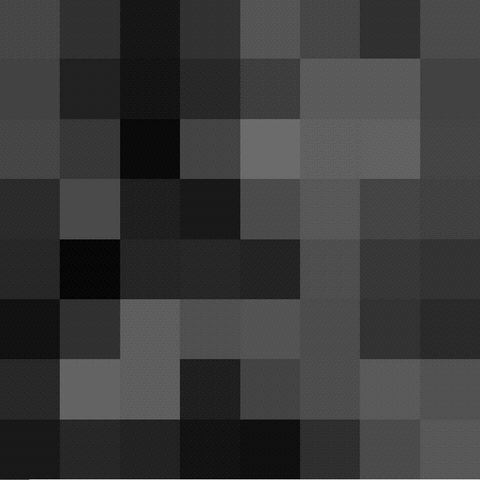Repitiendo tres pasos más, obtenemos las siguientes imágenes:Tras este paso, tenemos 1 + 4 + 16 + 64 + 256 + 1024 = 1365 coeficientes. ¿Se va pareciendo al original? Un poco, ¿verdad? Dos pasos más de nuestro algoritmo, y conseguimos, con 21845 coeficientes, una muy buena aproximación:
Dime que prefieres, ¿guardar una imagen en tu disco duro usando 21845 bytes, o los 1048576 originales? El algoritmo aquí presentado es uno de los más burdos que se puede imaginar. Además he usado para la descomposición los wavelets más sencillos y con menos propiedades que existen; las ondículas de Haar. Aún así, se observa con todo detalle lo potente que puede llegar a convertirse este esquema funcional, no sólo para aplicaciones prácticas, sino también como generador de descomposiciones que nos permitirán demostrar teoremas de forma muy intuitiva y constructiva… como jugar con el Lego.

Technorati Tags: matemáticas, math, wavelets